Joel Specter (Northwestern)
Commuting Endomorphisms of the p-adic Formal Disk
Any one dimensional formal group law over 
is uniquely determined by the series expansion of its multiplication by 
map. This talk addresses the converse question: when does an endomorphism 
of the 
-adic formal disk arise as the multiplication by 
-map of a formal group? Lubin, who first studied this question, observed that if such a formal group were to exist, then 
would commute with an automorphism of infinite order. He formulated a conjecture under which a commuting pair of series should arise from a formal group. Using methods from p-adic Hodge theory, we prove the height one case of this conjecture.
Bruce Berndt (UIUC)
Identities
As the title suggests, this lecture features mathematical identities. The identities we have chosen (we hope) are interesting, fascinating, surprising, and beautiful! Many of the identities are due to Ramanujan. Topics behind the identities include partitions, continued fractions, sums of squares, theta functions, Bessel functions, 
-series, other infinite series, and infinite integrals.
Matthias Strauch (Indiana)
Coverings of the p-adic upper half plane and arithmetic differential operators
The p-adic upper half plane comes equipped with a remarkable tower of GL(2)-equivariant etale covering spaces, as was shown by Drinfeld. It has been an open question for some time whether the spaces of global sections of the structure sheaf on such coverings provide admissible locally analytic representations. Using global methods and the p-adic Langlands correspondence for GL(2,Qp), this is now known to be the case by the work of Dospinescu and Le Bras. For the first layer of this tower Teitelbaum exhibited a nice formal model which we use to provide a local proof for the admissibility of the representation (when the base field is any finite extension of Qp). The other key ingredients are suitably defined sheaves of arithmetic differential operators and D-affinity results for formal models of the rigid analytic projective line, generalizing those of Christine Huyghe. This is joint work with Deepam Patel and Tobias Schmidt.
Amita Malik (UIUC)
Partitions into 
th powers of a fixed residue class
G. H. Hardy and S. Ramanujan established an asymptotic formula for the number of unrestricted partitions of a positive integer, and claimed a similar asymptotic formula for the number of partitions into perfect 
th powers, which was later proved by E. M. Wright. In this talk, we discuss partitions into parts from a specific set 
, for fixed positive integers 
, 
and 
. We give an asymptotic formula for the number of such partitions, thus generalizing the results of Wright and others. We also discuss the parity problem for such partitions. This is joint work with Bruce Berndt and Alexandru Zaharescu.
Brad Rodgers (Michigan)
Sums in short intervals and decompositions of arithmetic functions
In this talk we will discuss some old and new conjectures about the behavior of sums of arithmetic functions in short intervals, along with analogues of these conjectures in a function field setting that have been proved in recent years. We will pay particular attention to some surprising phenomena that comes into play, and a decomposition of arithmetic functions in a function field setting that helps elucidate what's happening.
Frank Garvan (Florida)
New Mock Theta Function Identities
In his last letter to Hardy, Ramanujan defined ten mock theta functions of order 5 and three of order 7. He stated that the three mock theta functions of order 7 are not related. We give simple proofs of new Hecke double sum identities for two of the order 5 functions and all three of the order 7 functions. We find that the coefficients of Ramanujan's three mock theta functions of order 7 are surprisingly related.
Sudhir Pujahari (Harish-Chandra Institute)
In the neighbourhood of Sato-Tate conjecture
In this talk, we will see the distribution of gaps between eigenangles of Hecke operators acting on the space of cusp forms of weight 
and level 
, spaces of Hilbert modular forms of weight 
and space of primitive Maass forms of weight 
. Moreover, we will see the following: Let 
and 
be two normalized Hecke eigenforms of weight 
and 
such that one of them is not of CM type. If the set of primes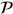 
such that the 
-th coefficients of 
and 
matches has positive upper density, then 
is a Dirichlet character twist of 
. The last part is a joint work with M. Ram Murty
Armin Straub (South Alabama)
A gumbo with hints of partitions, modular forms, special integer sequences and supercongruences
Euler's partition theorem famously asserts that the number of ways to partition an integer into distinct parts is the same as the number of ways to partition it into odd parts. In the first part of this talk, we describe a new analog of this theorem for partitions of fixed perimeter. More generally, we discuss enumeration results for simultaneous core partitions, which originates with an elegant result due to Anderson that the number of 
-core partitions is finite and is given by generalized Catalan numbers.
The second part is concerned with congruences between truncated hypergeometric series and modular forms. Specifically, we discuss a supercongruence modulo 
between the 
th Fourier coefficient of a weight 6 modular form and a truncated 
-hypergeometric series. The story is intimately tied with Apéry's proof of the irrationality of 
. This is recent joint work with Robert Osburn and Wadim Zudilin.
Preston Wake (UCLA)
Pseudorepresentations and the Eisenstein ideal
In his landmark 1976 paper "Modular curves and the Eisenstein ideal", Mazur studied congruences modulo p between cusp forms and an Eisenstein series of weight 2 and prime level N. He proved a great deal about these congruences, but also posed a number of questions: how big is the space of cusp forms that are congruent to the Eisenstein series? How big is the extension generated by their coefficients? In joint work with Carl Wang Erickson, we give an answer to these questions using the deformation theory of Galois pseudorepresentations. The answer is intimately related to the algebraic number theoretic interactions between the primes N and p, and is given in terms of cup products (and Massey products) in Galois cohomology.
Bao V. Le Hung (U Chicago)
Congruences between automorphic forms
The theory of congruences between automorphic forms traces back to Ramanujan, who observed various congruence properties between coefficients of generating functions related to the partition function. Since then, the subject has evolved to become a central piece of contemporary number theory; lying at the heart of spectacular achievements such as the proof of Fermat's Last Theorem and the Sato-Tate conjecture. In my talk I will explain how the modern theory gives satisfactory explanations of some concrete congruence phenomena for modular forms (the 
case), as well as recent progress concerning automorphic forms for higher rank groups. This is joint work with D. Le, B. Levin and S. Morra.
Matt Papanikolas (Texas A&M)
Limits of function field Bernoulli-Carlitz numbers
Because of the classical Kummer congruences, one is able to take p-adic limits of certain natural subsequences of Bernoulli numbers. This leads to notions of p-adic limits of special zeta values and Eisenstein series. In the case of the rational function field K over a finite field, the analogous quantities, called Bernoulli-Carlitz numbers, fail to satisfy Kummer-type congruences. Nevertheless, we prove that certain subsequences of Bernoulli-Carlitz numbers do have v-adic limits, for v a finite place of K, thus leading to new v-adic limits of Eisenstein series. Joint with G. Zeng.
Robert Lemke Oliver (Tufts)
Unexpected biases in the distribution of consecutive primes
While the sequence of primes is very well distributed in the reduced residue classes (mod q), the distribution of pairs of consecutive primes among the permissible pairs of reduced residue classes (mod q) is surprisingly erratic. We propose a conjectural explanation for this phenomenon, based on the Hardy-Littlewood conjectures, which fits the observed data very well. We also study the distribution of the terms predicted by the conjecture, which proves to be surprisingly subtle. This is joint work with Kannan Soundararajan.
Andrew Sills (Georgia Southern)
A formula for the partition function that "counts"
A partition of an integer n is a representation of n as a sum of positive integers where the order of the summands is considered irrelevant. Thus we see that there are five partitions of the integer 4, namely 4, 3+1, 2+2, 2+1+1, 1+1+1+1. The partition function p(n) denotes the number of partitions of n. Thus p(4) = 5. The first exact formula for p(n) was given by Hardy and Ramanujan in 1918. Twenty years later, Hans Rademacher improved the Hardy-Ramanujan formula to give an infinite series that converges to p(n). The Hardy-Ramanujan-Rademacher series is revered as one of the truly great accomplishments in the field of analytic number theory. In 2011, Ken Ono and Jan Bruinier surprised everyone by announcing a new formula which attains p(n) by summing a finite number of complex numbers which arise in connection with the multiset of algebraic numbers that are the union of Galois orbits for the discriminant -24n + 1 ring class field. Thus the known formulas for p(n) involve deep mathematics, and are by no means "combinatorial" in the sense that they involve summing a finite or infinite number of complex numbers to obtain the correct (positive integer) value. In this talk, I will show a new formula for the partition function as a multisum of positive integers, each term of which actually counts a certain class of partitions, and thus appears to be the first truly combinatorial formula for p(n). The idea behind the formula is due to Yuriy Choliy, and the work was completed in collaboration with him. We will further examine a new way to approximate p(n) using a class of polynomials with rational coefficients, and observe this approximation is very close to that of using the initial term of the Rademacher series. The talk will be accessible to students as well as faculty, and anyone interested is encouraged to attend!
Iván Blanco-Chacón (University College Dublin)
Hida Families, Hilbert Modular Forms and Arithmetic Applications
Part I will be an introduction to p-adic modular forms and Hida families for GL(1). In Part II we discuss Hilbert modular forms and Hida families of Hilbert modular forms for GL(2). Part III will focus on Hirzebruch-Zagier cycles and a p-adic Gross-Zagier formula.